I haven’t written any Photoshop tutorials for a while. Today I’m going to share a simple tutorial on how to create reusable background patterns with Photoshop and CSS. I learned this trick from designing WordPress themes. The trick is to create one reusable transparent PNG background and use CSS background-color property to create various color skins. It is particularly useful for creating customizable and dynamic templates (see demos).
What is so cool about this?
With transparent pattern image, users can easily customize the background color by altering the hex color.

Photoshop Trick: Extracting Pattern
This Photoshop trick works on most pattern images. For this demonstration, I’m going to use a tiled pattern image below. Follow the steps below to extract the pattern from the image. You will learn how to use Photoshop Channels to create selection.

Step 1
First you have to turn the image layer to black & white (go to Image > Adjustments > Destaturate). Then go to Image > Adjustments > Levels. Slide the: shadow, midtone, and highlight stopper to adjust the level. The goal here is to make the transparent area completely white.
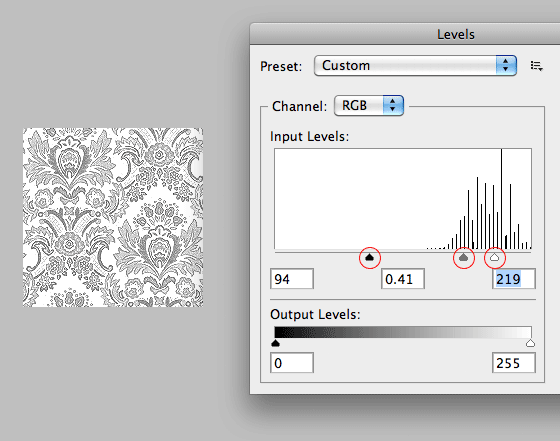
Step 2
Now you should have a black & white pattern. Go to Image > Adjustments > Invert (or press Cmd + I for shortcut). Select all and copy the pattern. Go to the Channels palette, add a new Channel and then paste the pattern into the Channel layer. Remember: the white pixel in the Channel layer will be the selection.

Step 3
Go back to the Layers palette. Create a new layer. Go to Selection > Load Selection and select the Channel that you’ve just created in the previous step. Then fill the selection with a solid color (eg. black).
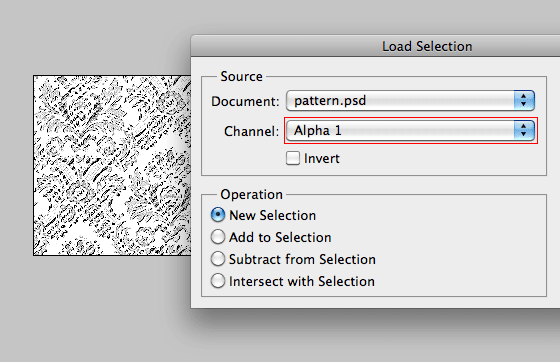
Shortcut tip for loading the Channel selection: hold down the Cmd key and click on the Channel layer thumbnail. Learn more Photoshop shortcuts here.
Opacity
To control the instensity or the darkness of the pattern, adjust the layer’s opacity.

Final (see demos)
Save the final pattern as a transparent PNG file. Now you may use CSS to easily change the background color to any hex code.
.pattern {
background-image: url(pattern.png);
background-color: #666;
}
ron
good tutorial, but instead of copying and pasting, just select the most contrasted chanel duplicate it and then use the levels. that is my way.just less steps.
Craig
How is the browser compatibility?
Joel Drapper
I think it covers every browser made within the last 10 years pretty much. Even IE6 if you use one of the IE6 PNG fixes http://24ways.org/2007/supersleight-transparent-png-in-ie6
Lisa
If someone is using a browser that can’t support a simple function such as this one, they probably don’t care about aesthetics in general.
Kalen
Thanks Nick. Working on a new site and am just now getting around to tweaking the design- have been working mostly on the DB and function. I like this approach to making some backgrounds with depth and flexibility.
minisite templates
Hmm, this is really worth reading post, thanks for posting….
Gaurav
very nice tutorial… Thanks for sharing.
Jon
Good application of this technique. I use this all the time when clients send me their logos as jpegs and don’t have access to source files. I usually can get rid of a white background in a matter of seconds.
Lumix
Very nifty tutorial. Now I know how to create my very own background pattern for my website. :) I’m thinking of changing my background soon!
jehzlau
Nice…! I’ll make one now based on this tut! :)
Simon
Hi
Thanks for this. I am just getting into WordPress blogs and want to get into designing my own themes.
Thanks
Simon
Colchester, UK
Steve Cook
Great idea. Although I’m not sure what use it might be, you could use jQuery to dynamically vary the background color within a set range.
Gaurav Mishra
This is REALLY SO GOOD!
ข่าวบันเทิงเกาหลี
Nice tutorial. I’ll try this in my next website.
sonali
I found it really useful thnx.
Tobias
Thanks for this, i use the same technique for a website but i’m searching for a solution to change the color of the pattern itself – i mean it should be possible to change the background color and the pattern color … do you know a solution without HTML5 …
Andy
Very useful, especially when prototyping. How would you do this in Fireworks?
Sampson Orson Jackson
Great post and nice timing.
M Francis
Cool trick… I actually use this on my sites sometimes.
billseymour
Very useful. Many thanks for sharing.
Kieran Daly
Thanks for this. There seems to be a huge push for this type of pattern these days and I see it all the time in the newer WordPress themes that are out there.
What is driving this change. Up to a few years ago it was flat backgrounds but its lieka stampede t ocreate this type of thing.
Don’t get me wrong I think they are OK and this tutorial is the first I have seen on how to do it but when eery theme on the block has it it is like Pamplona running the buuls :-)
Damian
Thanks keep em coming
Umer Malik
Excellent post for web designers.
Sökmotoroptimering
Thanx for this useful tips.
Its a good tutorial.
Milwaukee Web Design
Cool trick. Does this work with GIF’s as well?
Ali
Good tutorial
Thank you!
Ali
Thank you
That was cool
珠海男科医院
路过踩一踩,表示我来过
支持你的博客https://webdesignerwall.mystagingwebsite.com/
也谢谢您的回访http://nanke.zhwjyy.com/?wyxn3tj3
art
mena shaung
YourTubeTheme
Nice technique, I really like how the user can switch colors and still get the same pattern that you’ve created for them.
iphone 4 case
I’d have to check with you here. Which is not something I usually do! I enjoy reading a post that will make people think. Also, thanks for allowing me to comment! thank you!
andischroeder
thanks for the tutorial. Can you tell me how to add this to my twitter page?
thanks, Andi
Jonathan
I use a very similar technique to this for backgrounds, but I set it up with 2 divs so that I can set the opacity on the pattern and the background color separately. It’s a bit more verbose, but a bit more flexible (which, imo, is a good tradeoff in a wordpress theme)
Jasa Pembuatan Web
Beautiful Pattern.. thanks for share…
Chantelle
Fantastic and useful tips. The Radiolab site has one of my favorite backgrounds check it out http://browsingideas.com/radiolab-surreal-quirky-engaging/
Devon Wedding Photohrapher
Great tutorial. Thanks for posting. Really helpful info, clearly explained.
Andronicus Riyono
Combine the darkest pattern from this page with CSS background image hack: Emulating background-opacity from http://nicolasgallagher.com/css-background-image-hacks/ then you’ll get more possibilities with just a single image. :)
Callum
If you have Adobe Fireworks it’s a one step process.
Simply import your pattern and choose Filters > Other > Convert to Alpha.
This removes the white background. No pixels are harmed in the process, so you get a nice, clean, crisp transparent pattern. :)
Régis Kuckaertz
Fireworks users may spare a few steps using Filters > Other > Convert to Alpha on the image. Very useful!
zohaib
well defined and very useful..
Jasper
This is great!
One extra thing that I like to do is sorta combine the “light” and “dark” versions of the pattern, so that the final image includes both black, white, and transparency.
It’s more confusing to make, but then you get a texture that has less effect on the color you tile it over. (In your demo, the “light” textures are much lighter in color than the dark ones)
Here’s the one I made: http://cl.ly/2s443k3A1o2f0d0Y2N0O
Layered over a saturated color, it changes the lightness very little, keeping the original background color more intact.
Free Sick Wallpapers
http://www.freesickwallpapers.com/
Check this out everyone Featured Wallpapers
Especially to suit your Mobile Phone!!
sundar
Cool & Useful….
sundar
Qutehue web design & development Studio
shan
Really nice demos..
Web Design company India
Web Design - Jared
Nice tutorial. That pattern reminds me of my grandparents wallpaper. ;)
Jane
Very nice collection for web design.
Brisbane Osteo
Awesome! Very cool, thanks for posting!
kangtanto
a really nice trick in using transparent background. Never thought about it…
Sara
I love this tutorial but I was wondering what would be the best way to make this a background pattern that would keep repeating itself as you scroll down a website? I’d be afraid the lines wouldn’t match and you’d see a difference between each repeat.
Biev
I don’t think you’d want that all over your website, though : / That would be really overkill, unless you’re going for the “grandma’s kitchen wall” effect! But if you look at the picture, there are only two symbols repeated and all of their respective bits and pieces are present in the selection, so it’s just a matter of putting the puzzle back together, then cropping carefully and setting the background to repeat.
avihay
Very nice. i love simple stuff to work with.
azz
where can i find other pattern in photoshop?
Maverick
wow, this is such a nice trick! very impressive!
Nancy Andrews
I am a newbie in photoshop and your tutorial helped me in becoming close to pro at creating beautiful templates.Thanks a lot.
MOB Design Group
Although still a struggle, I finally might get this one to work properly!! Thanks for link to shortcuts as well that’s a nice bonus.
Joe
kwel!!! thanks for sharing!!! :D nice work
mybookmart
nice one thanks for sharing it
Md Shahnur Arefin
Photoshop looks always very difficult to me. I am little confused how to start.
Maypre
This is really cool. This is something that we can be used for website owners who like to make color changes to their site but still maintain their companies branding.
Humera
Awesome! thank you for sharing
Web Design Malaysia
Great read. thanks for this!
adumpaul
Realy impressive design
Translation Services
The second demo pattern is great, a good background makes a website more appealing and attractive.
Sü Smith
Super fun tut! I just recently made up some seamless subtle textures to use as tiles in PS, but haven’t tried incorporating the textures as an overlay to a colored background in a website yet. I’m looking forward to playing around with this. :)
Endy
awesome…make pattern looks transparant
(sorry for my english..)
sdsf
aasdds
adumpaul
Awesome tutorial.Thank you for sharing.
Προώθηση Ιστοσελίδων
thanks a lot for the tutorial…
Will
This is great! So easy to follow, thank you so much for sharing
buy season 11 gladiator
the pattern is ultimate like it.
Audee
I just made a quick try to extract the pattern and very excited with the result :) ~ It will save time-load for a website with tiny transparent .png file and simple CSS to make it works!
Much thanks for sharing this idea & tips ;)
M.H.Awan
Super cool man.Blogger Tricks.
Aniket - Freelance Web Designer
Really nice stuff.
Having a common background structure helps create a sense of continuity & have a variation with different textures on different pages, is a cool thing to do.
Thanks for sharing a great tutorial.
Web Designer Dubai
Really usefull stuff, Never find pattern background so easy and explanatory. Nice article. Look back later for more information. Thanks a lot.
Michel
Awesome, nice work
Life insurance for Diabetics
Amazing.. love this thanks!! ;)
Trin CArl
Great Idea…with the design, I hope u don’t mind me adding your web page to my blog for future reference, keep it up!!!!!
Omeganova
What a great idea!
THX from Austria
Jessica Lee
Wonderful tutorial, thank you! I wish I’d found this years ago. :)
Thiet ke logo
This is what I need, this article details, very useful
heather
Thanks for the tutorial! Very detailed. Also having it set in lower transparency makes the pattern more subtle so it isn’t competing with the other images on the website (great for image heavy sites btw)
Joe John
Thanks for sharing…. BTW i like your header image.
Ibiza yates
Having a common background structure helps create a sense of continuity & have a variation with different textures on different pages, is a cool thing to do.
ACS
Buy Wow gold, Buy arena rating, buy arena carry
Afzal
Wow!,,Look so great and interesting,,Thank you much!,,,,